1    

2    

3    

4    

5    

6    

Detection Theory

Let’s continue from Chapter 3, where you are the data scientist building the loan approval model for the (fictional) peer-to-peer lender ThriveGuild. As then, you are in the first stage of the machine learning lifecycle, working with the problem owner to specify the goals and indicators of the system. You have already clarified that safety is important, and that it is composed of two parts: basic performance (minimizing aleatoric uncertainty) and reliability (minimizing epistemic uncertainty). Now you want to go into greater depth in the problem specification for the first part: basic performance. (Reliability comes in Part 4 of the book.)

What are the different quantitative metrics you could use in translating the problem-specific goals (e.g. expected profit for the peer-to-peer lender) to machine learning quantities? Once you’ve reached the modeling stage of the lifecycle, how would you know you have a good model? Do you have any special considerations when producing a model for risk assessment rather than simply offering an approve/deny output?

Machine learning models are decision functions: based on the borrower’s features, they decide a response that may lead to an autonomous approval/denial action or be used to support the decision making of the loan officer. The use of decision functions is known as statistical discrimination because we are distinguishing or differentiating one class label from the other. You should contrast the use of the term ‘discrimination’ here with unwanted discrimination that leads to systematic advantages to certain groups in the context of algorithmic fairness in Chapter 10. Discrimination here is simply telling the difference between things. Your favorite wine snob talking about their discriminative palate is a distinct concept from racial discrimination.

This chapter begins Part 3 of the book on basic modeling (see Figure 6.1 to remind yourself of the lay of the land) and uses detection theory, the study of optimal decision making in the case of categorical output responses,[1] to answer the questions above that you are struggling with.

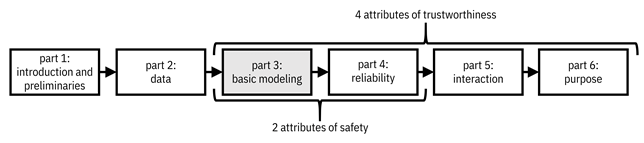
Figure 6.1. Organization of the book. This third part focuses on the first attribute of trustworthiness, competence and credibility, which maps to machine learning models that are well-performing and accurate. Accessible caption. A flow diagram from left to right with six boxes: part 1: introduction and preliminaries; part 2: data; part 3: basic modeling; part 4: reliability; part 5: interaction; part 6: purpose. Part 3 is highlighted. Parts 3–4 are labeled as attributes of safety. Parts 3–6 are labeled as attributes of trustworthiness.

Specifically, this chapter focuses on:

§  selecting metrics to quantify the basic performance of your decision function (including ones that summarize performance across operating conditions),

§  testing whether your decision function is as good as it could ever be, and

§  differentiating performance in risk assessment problems from performance in binary decision problems.

 

6.1           Selecting Decision Function Metrics

You, the ThriveGuild data scientist, are faced with the binary detection problem, also known as the binary hypothesis testing problem, of predicting which loan applicants will default, and thereby which applications to deny.[2] Let  be the loan approval decision with label  corresponding to  and label  corresponding to . Feature vector  contains employment status, income, and other attributes. The value  is called a negative and the value  is called a positive. The random variables for the features and label are governed by the pmfs given the special name likelihood functions  and , as well as by prior probabilities  and . The basic task is to find a decision function  that predicts a label from the features.[3]

6.1.1        Quantifying the Possible Events

There are four possible events in the binary detection problem:

1.    the decision function predicts  and the true label is ,

2.    the decision function predicts  and the true label is ,

3.    the decision function predicts  and the true label is , and

4.    the decision function predicts  and the true label is .

These are known as true negatives (TN), false negatives (FN), true positives (TP), and false positives (FP), respectively. A true negative is denying an applicant who should be denied according to some ground truth, a false negative is denying an applicant who should be approved, a true positive is approving an applicant who should be approved, and a false positive is approving an applicant who should be denied. Let’s organize these events in a table known as the confusion matrix:

 

Equation 6.1

The probabilities of these events are:

 

Equation 6.2

These conditional probabilities are nothing more than a direct implementation of the definitions of the events. The probability  is known as the true negative rate as well as the specificity and the selectivity. The probability  is known as the false negative rate as well as the probability of missed detection and the miss rate. The probability  is known as the true positive rate as well as the probability of detection, the recall, the sensitivity, and the power. The probability  is known as the false positive rate as well as the probability of false alarm and the fall-out. The probabilities can be organized in a slightly different table as well:

 

Equation 6.3

These probabilities give you some quantities by which to understand the performance of the decision function . Selecting one over the other involves thinking about the events themselves and how they relate to the real-world problem. A false positive, approving an applicant who should be denied, means that a ThriveGuild lender has to bear the cost of a default, so it should be kept small. A false negative, denying an applicant who should be approved, is a lost opportunity for ThriveGuild to make a profit through the interest they charge.

The events above are conditioned on the true label. Conditioning on the predicted label also yields events and probabilities of interest in characterizing performance:

 

Equation 6.4

These conditional probabilities are reversed from Equation 6.2. The probability  is known as the negative predictive value. The probability  is known as the false omission rate. The probability  is known as the positive predictive value as well as the precision. The probability  is known as the false discovery rate. If you care about the quality of the decision function, focus on the first set (, , , ). If you care about the quality of the predictions, focus on the second set (, , , ).

When you need to numerically compute these probabilities, apply the decision function to several i.i.d. samples of  and denote the number of TN, FN, TP, and FP events as , , , and , respectively.  Then use the following estimates of the probabilities:

 

 

Equation 6.5

As an example, let’s say that ThriveGuild makes the following number of decisions: , , , and . You can estimate the various performance probabilities by plugging these numbers into the respective expressions above. The results are , , , , , , , and . These are all reasonably good values, but must ultimately be judged according to the ThriveGuild problem owner's goals and objectives.

6.1.2        Summary Performance Metrics

Collectively, false negatives and false positives are errors. The probability of error, also known as the error rate, is the sum of the false negative rate and false positive rate weighted by the prior probabilities:

Equation 6.6

The balanced probability of error, also known as the balanced error rate, is the unweighted average of the false negative rate and false positive rate:

Equation 6.7

They summarize the basic performance of the decision function. Balancing is useful when there are a lot more data points with one label than the other, and you care about each type of error equally. Accuracy, the complement of the probability of error: , and balanced accuracy, the complement of the balanced probability of error: , are sometimes easier for problem owners to appreciate than error rates.

The -score, the harmonic mean of  and , is an accuracy-like summary measure to characterize the quality of a prediction rather than the decision function:

Equation 6.8

Continuing the example from before with  and , let ThriveGuild’s prior probability of receiving applications to be denied according to some ground truth be  and applications to be approved be . Then, plugging in to the relevant equations above, you’ll find ThriveGuild to have , , and . Again, these are reasonable values that may be deemed acceptable to the problem owner.

As the data scientist, you can get pretty far with these abstract TN, FN, TP, and FP events, but they have to be put in the context of the problem owner’s goals. ThriveGuild cares about making good bets on borrowers so that they are profitable. More generally across real-world applications, error events yield significant consequences to affected people including loss of life, loss of liberty, loss of livelihood, etc. Therefore, to truly characterize the performance of a decision function, it is important to consider the costs associated with the different events. You can capture these costs through a cost function  and denote the costs as , , , and , respectively.

Taking costs into account, the characterization of performance for the decision function is known as the Bayes risk :

Equation 6.9

Breaking the equation down, you’ll see that the two error probabilities,  and  are the main components, multiplied by their relevant prior probabilities and costs. The costs of the non-error events appear just multiplied by their costs. The Bayes risk is the performance metric most often used in finding optimal decision functions. Actually finding the decision function is known as solving the Bayesian detection problem. Eliciting the cost function  for a given real-world problem from the problem owner is part of value alignment, described in Chapter 14.

A mental model or roadmap, shown in Figure 6.2, to hold throughout the rest of the chapter is that the Bayes risk and the Bayesian detection problem are the central concept, and all other concepts are related to the central concept in various ways and for various purposes. The terms and concepts that have not yet been defined and evaluated are coming up soon.

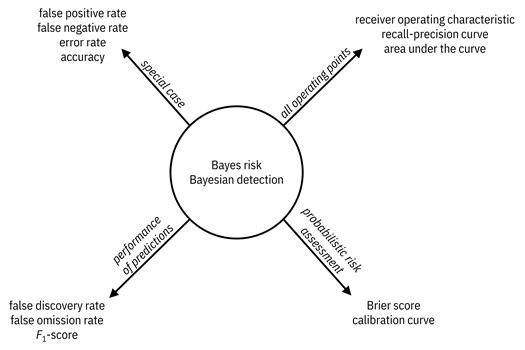
Figure 6.2. A mental model for different concepts in detection theory surrounding the central concept of Bayes risk and Bayesian detection. A diagram with Bayes risk and Bayesian detection at the center and four other groups of concepts radiating outwards. False positive rate, false negative rate, error rate, and accuracy are special cases. Receiver operating characteristic, recall-precision curve, and area under the curve arise when examining all operating points. Brier score and calibration curve arise in probabilistic risk assessment. False discover rate, false omission rate, and -score relate to performance of predictions.

Because getting things right is a good thing, it is often assumed that there is no cost to correct decisions, i.e.,  and , which is also assumed in this book going forward. In this case, the Bayes risk simplifies to:

Equation 6.10

To arrive at this simplified equation, just insert zeros for  and  in Equation 6.9. The Bayes risk with  and  is the probability of error.

We are implicitly assuming that  does not depend on  except through . This assumption is not required, but made for simplicity. You can easily imagine scenarios in which the cost of a decision depends on the feature. For example, if one of the features used in the loan approval decision by ThriveGuild is the value of the loan, the cost of an error (monetary loss) depends on that feature. Nevertheless, for simplicity, we usually make the assumption that the cost function does not explicitly depend on the feature value. For example, under this assumption, the cost of a false negative may be  and the cost of a false positive  for all applicants.

6.1.3        Accounting for Different Operating Points

The Bayes risk is all well and good if there is a fixed set of prior probabilities and a fixed set of costs, but things change. If the economy improves, potential borrowers might become more reliable in loan repayment. If a different problem owner comes in and has a different interpretation of opportunity cost, then the cost of false negatives  changes. How should you think about the performance of decision functions across different sets of those values, known as different operating points?

Many decision functions are parameterized by a threshold  (including the optimal decision function that will be demonstrated in Section 6.2). You can change the decision function to be more or less forgiving of false positives or false negatives, but not both at the same time. Varying  explores this tradeoff and yields different error probability pairs , i.e. different operating points. Equivalently, different operating points correspond to different false positive rate and true positive rate pairs . The curve traced out on the – plane as the parameter  is varied from zero to infinity is the receiver operating characteristic (ROC). The ROC takes values  when  and  when . You can understand this because at one extreme, the decision function always says ; in this case there are no FPs and no TPs. At the other extreme, the decision function always says ; in this case all decisions are either FPs or TPs.

The ROC is a concave, nondecreasing function illustrated in Figure 6.3. The closer to the top left corner it goes, the better. The best ROC for discrimination goes straight up to  and then makes a sharp turn to the right. The worst ROC is the diagonal line connecting  and  achieved by random guessing. The area under the ROC, also known as the area under the curve (AUC) synthesizes performance across all operating points and should be selected as a metric when it is likely that the same threshold-parameterized decision function will be applied in very different operating conditions. Given the shapes of the worst (diagonal line) and best (straight up and then straight to the right) ROC curves, you can see that the AUC ranges from  (area of bottom right triangle) to  (area of entire square).[4]

 

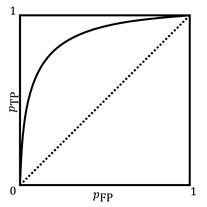
Figure 6.3. An example receiver operating characteristic (ROC). Accessible caption. A plot with  on the vertical axis and  on the horizontal axis. Both axes range from  to . A dashed diagonal line goes from  to  and corresponds to random guessing. A solid concave curve, the ROC, goes from  to  staying above and to the left of the diagonal line.

 

6.2           The Best That You Can Ever Do

As the ThriveGuild data scientist, you have given the problem owner an entire menu of basic performance measures to select from and indicated when different choices are more and less appropriate. The Bayes risk is the most encompassing and most often used performance characterization for a decision function. Let’s say that Bayes risk was chosen in the problem specification stage of the machine learning lifecycle, including selecting the costs. Now you are in the modeling stage and need to figure out if the model is performing well. The best way to do that is to optimize the Bayes risk to obtain the best possible decision function with the smallest Bayes risk and compare the current model’s Bayes risk to it.

“The predictability ceiling is often ignored in mainstream ML research. Every prediction problem has an upper bound for prediction—the Bayes-optimal performance. If you don't have a good sense of what it is for your problem, you are in the dark.”

—Mert R. Sabuncu, computer scientist at Cornell University

Let us denote the best possible decision function as  and its corresponding Bayes risk as . They are specified using the minimization of the expected cost:

Equation 6.11

where the expectation is over both  and . Because it achieves the minimal cost, the function  is the best possible  by definition. Whatever Bayes risk  it has, no other decision function can have a lower Bayes risk .

We aren’t going to work it out here, but the solution to the minimization problem in Equation 6.11 is the Bayes optimal decision function, and takes the following form:

Equation 6.12

where , known as the likelihood ratio, is defined as:

Equation 6.13

and , known as the threshold, is defined as:

Equation 6.14

The likelihood ratio is as its name says: it is the ratio of the likelihood functions. It is a scalar value even if the features  are multivariate. As the ratio of two non-negative pdf values, it has the range  and can be viewed as a random variable. The threshold is made up of both costs and prior probabilities. This optimal decision function  given in Equation 6.12 is known as the likelihood ratio test.

6.2.1        Example

As an example, let ThriveGuild’s loan approval decision be determined solely by one feature : the income of the applicant. Recall that we modeled income to be exponentially-distributed in Chapter 3. Specifically, let  and , both for . Like earlier in this chapter, , , , and . Then simply plugging in to Equation 6.13, you’ll get:

Equation 6.15

and plugging in to Equation 6.14, you’ll get:

Equation 6.16

Plugging these expressions into the Bayes optimal decision function given in Equation 6.12, you’ll get:

Equation 6.17

which can be simplified to:

Equation 6.18

by multiplying both sides of the inequalities in both cases by , taking the natural logarithm, and then multiplying by  again. Applicants with an income less than or equal to  are denied and applicants with an income greater than  are approved. The expected value of  is  and the expected value of  is . Thus in this example, an applicant's income has to be quite a bit higher than the mean to be approved.

You should use the Bayes-optimal risk  to lower bound the performance of any machine learning classifier that you might try for a given data distribution.[5] No matter how hard you work or how creative you are, you can never overcome the Bayes limit. So you should be happy if you get close. If the Bayes-optimal risk itself is too high, then the thing to do is to go back to the data understanding and data preparation stages of the machine learning lifecycle and get more informative data.

 

6.3           Risk Assessment and Calibration

To approve or to deny, that is the question for ThriveGuild. Or is it? Maybe the question is actually: what is the probability that the borrower will default? Maybe the problem is not binary classification, but probabilistic risk assessment. It is certainly an option for you, the data scientist, and the problem owner to consider during problem specification. Thresholding a probabilistic risk assessment yields a classification, but there are a few subtleties for you to weigh.

The likelihood ratio ranges from zero to infinity and the threshold value  is optimal for equal priors and equal costs. Applying any monotonically increasing function to both the likelihood ratio and the threshold still yields a Bayes optimal decision function with the same risk . That is,

Equation 6.19

for any monotonically increasing function  is still optimal.

It is somewhat more natural to think of a score  to be in the range  because it corresponds to the label values  and could also potentially be interpreted as a probability. The score, a continuous-valued output of the decision function, can then be thought of as a confidence in the prediction and be obtained by applying a suitable  function to the likelihood ratio. In this case,  is the threshold for equal priors and costs. Intermediate score values are less confident and extreme score values (towards  and ) are more confident. Just as the likelihood ratio may be viewed as a random variable, the score may also be viewed as a random variable . The Brier score is an appropriate performance metric for the continuous-valued output score of the decision function:

Equation 6.20

It is the mean-squared error of the score  with respect to the true label . For a finite number of samples , you can compute it as:

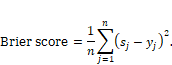
Equation 6.21

The Brier score decomposes into the sum of two separable components: calibration and refinement.[6] The concept of calibration is that the predicted score corresponds to the proportion of positive true labels. For example, a bunch of data points all having a calibrated score of  implies that 70% of them have true label  and 30% of them have true label . Said another way, perfect calibration implies that the probability of the true label  being  given the predicted score  being  is the value  itself:  Calibration is important for probabilistic risk assessments: a perfectly calibrated score can be interpreted as a probability of predicting one class or the other. It is also an important concept for evaluating causal inference methods, described in Chapter 8, for algorithmic fairness, described in Chapter 10, and for communicating uncertainty, described in Chapter 13.

Since any monotonically increasing transformation  can be applied to a decision function without changing its ability to discriminate, you can improve the calibration of a decision function by finding a better . The calibration loss quantitatively captures how close a decision function is to perfect calibration. The refinement loss is a sort of variance of how tightly the true labels distribute around a given score. For  that have been sorted by their score values and binned into  groups  with average values  within the bins

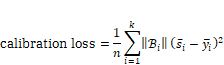
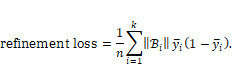
Equation 6.22

As stated earlier, the sum of the calibration loss and refinement loss is the Brier score.

A calibration curve, also known as a reliability diagram, shows the  values as a plot. One example is shown in Figure 6.4. The closer to a straight diagonal from  to , the better. Plotting this curve is a good diagnostic tool for you to understand the calibration of a decision function.

 

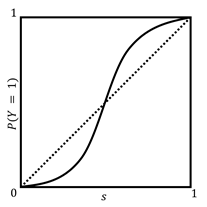
Figure 6.4. An example calibration curve. Accessible caption. A plot with on the vertical axis and  on the horizontal axis. Both axes range from  to . A dashed diagonal line goes from  to  and corresponds to perfect calibration. A solid S-shaped curve, the calibration curve, goes from  to  starting below and to the right of the diagonal line before crossing over to being above and to the left of the diagonal line.

 

6.4           Summary

§  Four possible events result from binary decisions: false negatives, true negatives, false positives, and true positives.

§  Different ways to combine the probabilities of these events lead to classifier performance metrics appropriate for different real-world contexts.

§  One important one is Bayes risk: the combination of the false negative probability and false positive probability weighted by both the costs of those errors and the prior probabilities of the labels. It is the basic basic performance measure for the first attribute of safety and trustworthiness.

§  Detection theory, the study of optimal decisions, which provides fundamental limits to how well machine learning models may ever perform is a tool for you to assess the basic performance of your models.

§  Decision functions may output continuous-valued scores rather than only hard, zero or one, decisions. Scores indicate confidence in a prediction. Calibrated scores are those for which the score value is the probability of a sample belonging to a label class.